Which polynomial represents the difference below? This question lies at the heart of understanding polynomial differences, a crucial concept in mathematical operations and beyond. Delve into this engaging exploration as we uncover the methods, examples, and applications of polynomial differences, unraveling their significance in various fields.
From defining polynomial differences and exploring their diverse representations to showcasing their practical applications, this comprehensive guide will illuminate the intricacies of this mathematical concept, leaving you with a profound understanding of its power and versatility.
1. Definition of Polynomial Difference: Which Polynomial Represents The Difference Below
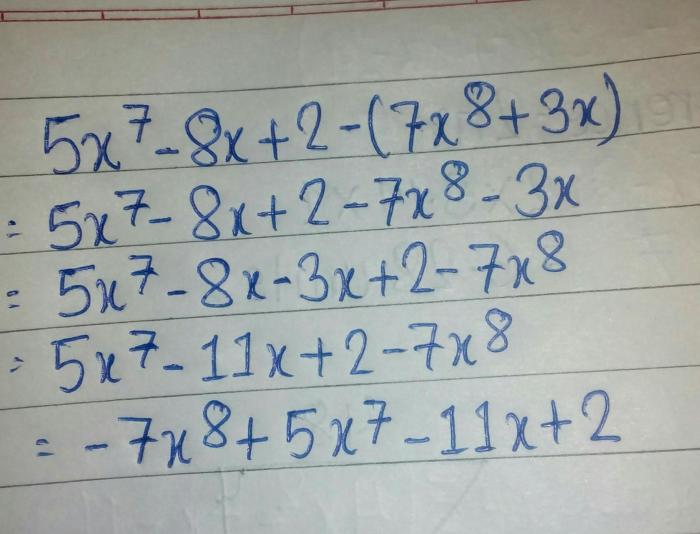
A polynomial difference refers to the subtraction of two polynomials, resulting in a new polynomial. This operation involves finding the difference between the coefficients of like terms in the two polynomials.
For example, consider the polynomials f(x) = 2x 2+ 3x – 5 and g(x) = x 2– 2x + 1. Their difference, f(x) – g(x), would be (2x 2– x 2) + (3x – (-2x)) + (-5 – 1) = x 2+ 5x – 6.
Polynomial differences are significant in mathematical operations as they allow for the simplification and manipulation of complex expressions. They are particularly useful in solving equations, finding roots, and performing other algebraic operations.
2. Methods for Representing Polynomial Differences
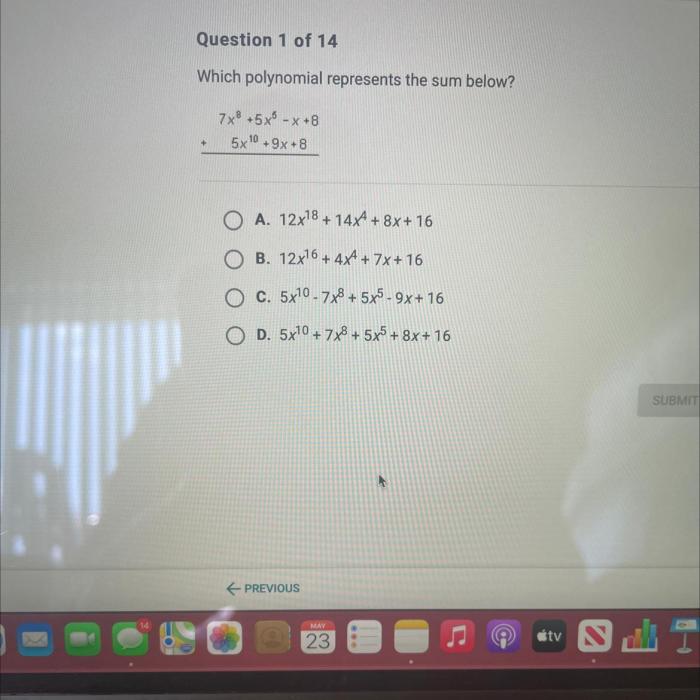
Polynomial differences can be represented using various methods, including:
- Horizontal Representation:Writing the polynomials one above the other and subtracting the coefficients of like terms.
- Vertical Representation:Placing the polynomials side by side and aligning the like terms vertically, then subtracting the coefficients.
- Using a Table:Creating a table with columns for the coefficients of each term and subtracting the corresponding values.
Each method has its advantages and disadvantages. Horizontal representation is straightforward and easy to understand, while vertical representation allows for easier alignment and comparison of terms. Using a table provides a clear and organized view of the coefficients.
3. Examples of Polynomial Differences

Consider the following polynomial differences:
| Polynomial 1 | Polynomial 2 | Difference |
|---|---|---|
f(x) = 3x3
|
g(x) = x3 + x2
|
2x3
|
h(x) = 2x4
|
k(x) = x4
|
x4+ x 3
|
These examples demonstrate the different ways in which polynomial differences can be calculated and represented.
4. Applications of Polynomial Differences
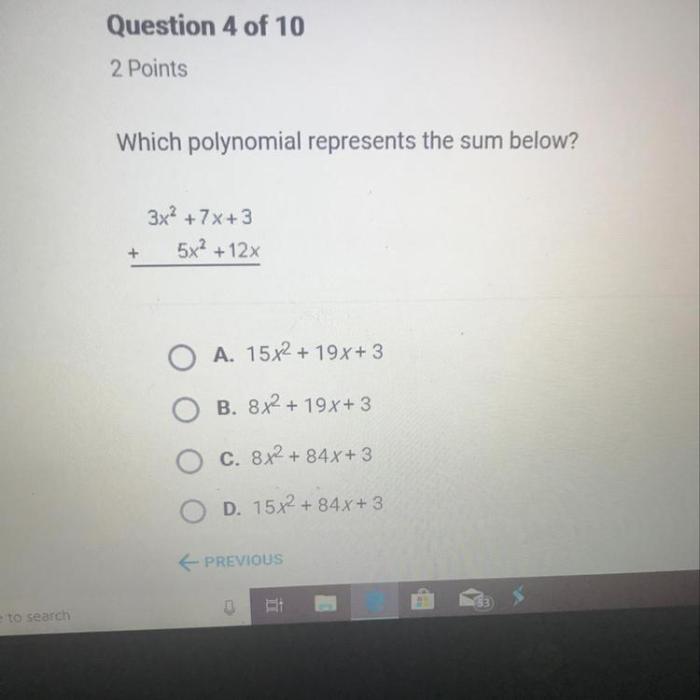
Polynomial differences have practical applications in various fields, including:
- Algebra:Simplifying expressions, solving equations, and finding roots.
- Calculus:Finding derivatives and integrals of polynomials.
- Computer Science:Evaluating polynomial functions and solving polynomial equations.
- Physics:Modeling physical phenomena using polynomial equations.
- Finance:Analyzing financial data and making investment decisions.
Polynomial differences provide a powerful tool for manipulating and understanding polynomial expressions, making them essential in a wide range of applications.
5. Extensions and Variations
The concept of polynomial differences can be extended and varied in several ways:
- Difference of Polynomials with Variables:Instead of constants, the coefficients can be variables, resulting in a polynomial difference with variables.
- Difference of Rational Functions:The polynomials can be replaced with rational functions, leading to a difference of rational functions.
- Difference of Polynomials over a Ring:The polynomials can be defined over a ring other than the real or complex numbers.
These extensions expand the applicability of polynomial differences and allow for more complex mathematical operations.
General Inquiries
What is a polynomial difference?
A polynomial difference is the result of subtracting one polynomial from another.
How can polynomial differences be represented?
Polynomial differences can be represented using tables, bullet points, or algebraic expressions.
What are the applications of polynomial differences?
Polynomial differences have applications in fields such as algebra, calculus, engineering, and computer science.
